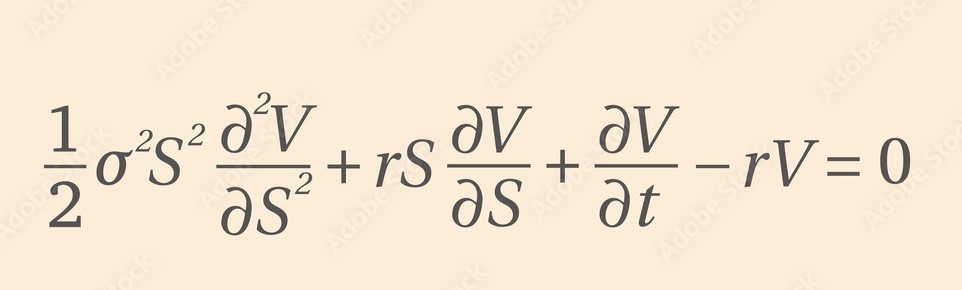In this post, I provide a derivation of the price of a European Call Option on a non-dividend paying stock in the Black-Scholes Model. This usually involves deriving the PDE first and expressing it as the Heat equation with a well-known closed-form solution. However, in this case, I will avoid Ito’s Lemma and solving the Black-Scholes PDE, taking an approach that might be more appealing for a statistician (but less for a physicist).
The price of the call option is given by the expected payoff under the risk-neutral measure:
$$C(K,0) = e^{-rT} E_{Q}\left[max(S_T – K , 0)\right]$$
$$= \underset{(2)}{\underbrace{e^{-rT} E_{Q}\left[S_T I(S_T>K)\right]}} – \underset{(1)}{\underbrace{e^{-rT} E_{Q}\left[K I(S_T>K)\right]}}$$
Using that \(S_t = S_0 e^{(r-\frac{1}{2}\sigma^2)t + \sigma B_t}\) we work in (1) to obtain an expression in terms of the Normal cdf:
$$e^{-rT} E_{Q}\left[K I(S_T>K)] = e^{-rT} K Q(S_T>K\right)$$
$$=e^{-rT} K Q\left(S_0 e^{(r-\frac{1}{2}\sigma^2)T + \sigma B_T}>K\right)=e^{-rT} K Q\left(ln(S_0) + (r-\frac{1}{2}\sigma^2)T + \sigma B_T>ln(K)\right)$$
$$=e^{-rT} K Q\left(B_T>\frac{ln(K/S_0) – (r-\frac{1}{2}\sigma^2)T}{\sigma}\right)=e^{-rT} K Q\left(B_T\leq \frac{ln(S_0/K) + (r-\frac{1}{2}\sigma^2)T}{\sigma}\right)$$
And using that under \(Q, B_T \sim N(0,T)\) we get:
$$=e^{-rT} K Q\left(\frac{B_T}{\sqrt{T}}>\frac{ln(S_0/K) + (r-\frac{1}{2}\sigma^2)T}{\sqrt{T}\sigma}\right)=e^{-rT} K \Phi\left(\frac{ln(S_0/K) + (r-\frac{1}{2}\sigma^2)T}{\sqrt{T}\sigma}\right)$$
Now we work in (2), trying to accomplish the same task:
$$e^{-rT} E_{Q}\left[I(S_T>K)\right]$$
$$=e^{-rT} E_{Q}\left[S_0 e^{(r-\frac{1}{2}\sigma^2)T + \sigma B_T} I(S_T>K)\right]=S_0 E_{Q}\left[e^{\sigma B_T – \frac{1}{2}\sigma^2T} I(S_T>K)\right]$$
Here is the key point of this approach. By Girsanov theorem, if \(B_t\) is a driftless Brownian motion under \(Q\), \(B_t -\sigma t\) is a driftless Brownian motion under another measure \(Q’\) characterized by the Radon-Nikodym derivative \(\frac{dQ’}{dQ}=e^{\sigma B_t – \frac{1}{2}\sigma^2 t}\). Therefore:
$$=S_0 E_{Q}\left[\frac{dQ’}{dQ} I(S_T>K)\right] = S_0 E_{Q’}\left[I(S_T>K)\right] = S_0 Q’\left(I(S_T>K)\right) $$
Isolating B_T:
$$S_0 Q’\left(I(S_T>K)\right)=S_0 Q’\left(S_0 e^{(r-\frac{1}{2}\sigma^2)T + \sigma B_T}>K \right)$$
$$=S_0 Q’ \left( B_T>\frac{ln(K/S_0) – (r-\frac{1}{2}\sigma^2)T}{\sigma}\right)$$
But B_T is not a Brownian undeer \(Q\), so we need work a bit more:
$$=S_0 Q’\left( \frac{B_T-\sigma T}{\sqrt{T}}>\frac{ln(K/S_0) – (r+\frac{1}{2}\sigma^2)T}{\sigma \sqrt{T}}\right)=S_0 Q’\left( \frac{B_T-\sigma T}{\sqrt{T}} \leq \frac{ln(S_0/K) + (r+\frac{1}{2}\sigma^2)T}{\sigma \sqrt{T}}\right)$$
$$=S_0 \Phi \left( \frac{ln(S_0/K) + (r+\frac{1}{2}\sigma^2)T}{\sigma \sqrt{T}}\right)$$
Finally, collecting the two expressions we get the closed form solution for the price of an European Call Option in the Black-Scholes model
$$C(K,0) = S_0 \Phi \left( \frac{ln(S_0/K) + T(r+\frac{1}{2}\sigma^2)}{\sigma \sqrt{T}}\right) – e^{-rT} K \Phi\left(\frac{ln(S_0/K) + (r-\frac{1}{2}\sigma^2)T}{\sigma \sqrt{T}}\right)$$